Testing Database Migration Scripts with Spring Boot and Testcontainers

Database migration with tools like Flyway or Liquibase requires creating SQL scripts and running them on a database. Although the database is an external dependency, we have to test the SQL scripts, because it is our code. But this code doesn’t run in the application that we develop and cannot be tested with unit tests.

This article shows how to test database migration scripts with Flyway and Testcontainers in a Spring Boot application and to keep the tests close to production.

Example Code

Key Takeaways

• Using an in-memory database for integration tests will cause compatibility issues in our SQL scripts between the in-memory database and the production database.
• Using Testcontainers, we can easily spin up a Docker container with the production database for our tests.

Common Practice

There is a very common and convenient approach for testing database migration scripts with Flyway at build time.

It’s a combination of Flyway migration support in Spring Boot and an in-memory database like H2. In this case, the database migration begins whenever the Spring application context starts, and the SQL scripts are executed on an H2 database with Flyway.

It’s easy and fast. But is it good?

The Problem of Using an In-Memory Database for Tests

H2 is usually not the database we use in production or other production-like environments. When we test the SQL scripts with the H2 database, we have no idea about how the migration would run in the production environment.

H2 has compatibility modes to disguise as other databases. This may include our production database. With these modes, we can start the H2 database and it will, for example, behave like a PostgreSQL database.

But there are still differences. The SQL code for an H2 might still look different from the code for PostgresSQL.

Let’s look at this SQL script:

CREATE TABLE car
(
  id  uuid PRIMARY KEY,
  registration_number VARCHAR(255),
  name  varchar(64) NOT NULL,
  color varchar(32) NOT NULL,
  registration_timestamp INTEGER
);

This script can run on an H2 as well as on a PostgreSQL database.

Now we want to change the type of the column registration_timestamp from INTEGER to timestamp with time zone and of course, we want to migrate the data in this column. So, we write an SQL script for migrating the registration_timestamp column:

ALTER TABLE car
  ALTER COLUMN registration_timestamp SET DATA TYPE timestamp with time zone
   USING
   timestamp with time zone 'epoch' +
    registration_timestamp * interval '1 second';

This script will not work for H2 with PostgreSQL mode, because the USING clause doesn’t work with ALTER TABLE for H2.

Depending on the database we have in production, we might have database-specific features in the SQL scripts. Another example would be using table inheritance in PostgreSQL with the keyword INHERITS, which isn’t supported in other databases.

We could, of course, maintain two sets of SQL scripts, one for H2, to be used in the tests, and one for PostgreSQL, to be used in production:

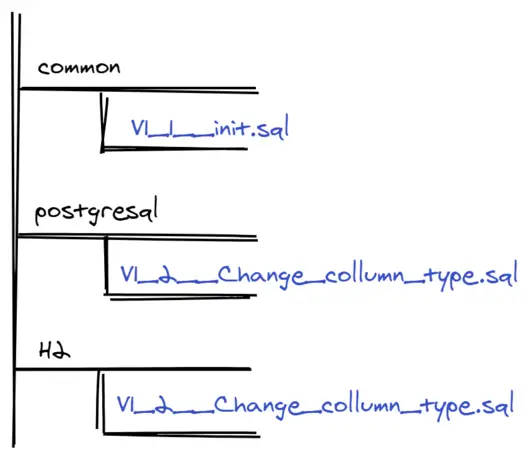
But now,:

• we have to configure Spring Boot profiles for different folders with scripts,
• we have to maintain two sets of scripts,
• and most importantly, we are not able to test scripts from the folder postgresql at build time.

If we want to write a new script with some features that are not supported by H2, we have to write two scripts, one for H2 and one for PostgreSQL. Also, we have to find a way to achieve the same results with both scripts.

If we test the database scripts with the H2 database, and our test is green, we don’t know anything about the script V1_2__change_column_type.sql from the folder postgresql.

These tests would give us a false sense of security!

Using a Production-Like Environment for Testing Database Scripts

There is another approach for testing database migration: we can test database migration with an H2 database at build time and then deploy our application into a production-like environment and let the migration scripts run on this environment with the production-like database, for example, PostgreSQL.

This approach will alert us if any scripts are not working with the production database, but it still has drawbacks:

• Bugs are discovered too late,
• it is hard to find errors,
• and we still have to maintain two sets of SQL scripts.

Let’s imagine that we test the migration with the H2 database during build-time of the application, and the tests are green. The next step is delivering and deploying the application to a test environment. It takes time. If the migration in the test environment fails, we’ll be notified too late, maybe several minutes later. This slows down the development cycle.

Also, this situation is very confusing for developers, because we can’t debug errors like in our unit test. Our unit test with H2 was green, after all, and the error only happened in the test environment.

Using Testcontainers

With Testcontainers we can test the database migration against a Docker container of the production database from our code. On the developer machine or the CI server.

Testcontainers is a Java library that makes it easy to start up a Docker container from within our tests.

Of course, we’ll have to install Docker to run it. After that, we can create some initialization code for testing:

@ContextConfiguration(
  initializers = AbstractIntegrationTest.Initializer.class)
public class AbstractIntegrationTest {

  static class Initializer implements 
       ApplicationContextInitializer<ConfigurableApplicationContext> {

    static PostgreSQLContainer<?> postgres = new PostgreSQLContainer<>();

    private static void startContainers() {
      Startables.deepStart(Stream.of(postgres)).join();
      // we can add further containers 
      // here like rabbitmq or other databases
    }

    private static Map<String, String> createConnectionConfiguration() {
      return Map.of(
          "spring.datasource.url", postgres.getJdbcUrl(),
          "spring.datasource.username", postgres.getUsername(),
          "spring.datasource.password", postgres.getPassword()
      );
    }


    @Override
    public void initialize(
        ConfigurableApplicationContext applicationContext) {
      
      startContainers();

      ConfigurableEnvironment environment = 
        applicationContext.getEnvironment();

      MapPropertySource testcontainers = new MapPropertySource(
          "testcontainers",
          (Map) createConnectionConfiguration()
      );

      environment.getPropertySources().addFirst(testcontainers);
    }
  }
} 

AbstractIntegrationTest is an abstract class that defines a PostgreSQL database and configures the connection to this database. Other test classes that need access to the PostgreSQL database can extend this class.

In the @ContextConfiguration annotation, we add an ApplicationContextInitializer that can modify the application context when it starts up. Spring will call the initialize() method.

Within initialize(), we first start the Docker container with a PostgreSQL database. The method deepStart() starts all items of the Stream in parallel. We could additional Docker containers, for instance, RabbitMQ, Keycloak, or another database. To keep it simple, we’re starting only one Docker container with the PostgreSQL database.

Next, we call createConnectionConfiguration() to create a map of the database connection properties. The URL to the database, username, and password are created by the Testcontainers automatically. Hence, we get them from the testcontainers instance postgres and return them.

It’s also possible to set these parameters manually in the code, but it’s better to let Testcontainers generate them. When we let Testcontainers generate the jdbcUrl, it includes the port of the database connection. The random port provides stability and avoids possible conflicts on the machine of another developer or a build server.

Finally, we add these database connection properties to the Spring context by creating a MapPropertySource and adding it to the Spring Environment. The method addFirst() adds the properties to the contexts with the highest precedence.

Now, if we want to test database migration scripts, we have to extend the class and create a unit test.

@SpringBootTest
class TestcontainersApplicationTests extends AbstractIntegrationTest {

  @Test
  void migrate() {
  // migration starts automatically,
  // since Spring Boot runs the Flyway scripts on startup
  }

}

The class AbstractIntegrationTest can be used not only for testing database migration scripts but also for any other tests that need a database connection.

Now we can test the migration of SQL scripts with Flyway by using a PostgreSQL database at build time.

We have all dependencies in our code and can spin up a close-to-production test environment anywhere.

Drawbacks

As we mentioned above, we have to install Docker on every machine where we want to build the application. This could be a developer laptop or a CI build server.

Also, tests interacting with Testcontainers are slower than the same test with an in-memory database, because the Docker container has to be spun up.

Conclusion

Testcontainers supports testing the application with unit tests using Docker containers with minimal effort.

Database migration tests with Testcontainers provide production-like database behavior and improve the quality of the tests significantly.

There is no need to use an in-memory database for tests.